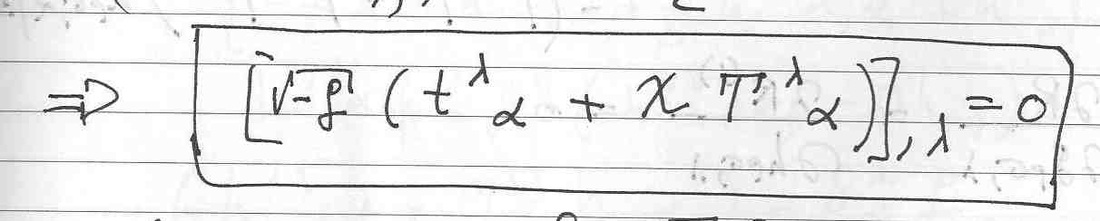Ricerca

Weak Field Limits and astrophysical applications of Extended Theories of Gravity

I try to carry out the following

Studying extended theories of gravity at galactic scales

Modifications of the gravitational potential alter the asymptotic Keplerian behaviour usually adopted and, when we consider ETG, a correction emerges and leads to a specific rotation curve. Assuming realistic models of the morphology of the galaxy and relaxing the thin disk assumption lead to interesting models to estimate the speed of rotation. Since the Newtonian limit derives from the linearization of the field equations, one can use the superposition principle and we obtain the effective gravitational potential in the galaxy. By comparing the theoretical results with experimental evidences we can obtain constraints on free parameters of the theory. Furthermore in this case it is possible to quantify the fluctuations in the vertical plane of the galaxy. This is only an initial analysis where a test body is embedded in the gravitational field of the galaxy, but the case of a collisionless stellar system can be further analyzed and the theoretical predictions about the formation of stellar clusters can be made. Then, a generalization of the Boltzmann equation and the Jeans instability can be formulated.

Testing extended theories of gravity under the assumption of hydrostatic equilibrium

The formation and especially the evolution of stars are other tests of the validity of ETGS and of their compatibility with current knowledge. Observed stellar structures are incompatible with the standard models of stellar structure. In particular, we refer to the neutron stars (magnetars [40]) with mass larger than the Volkoff mass. It therefore seems that on particular length scales the gravitational force is larger or smaller than the corresponding value in GR. For example, a modification of the Hilbert-Einstein Lagrangian consisting of an $R^2$ term enables a major attraction while a $R_{\alpha\beta} R^{\alpha\beta}$ term gives a repulsive contribution. Understanding on which scales the modifications to GR are activated or what is the weight of corrections to gravitational potential is a crucial point.

Developing the understanding of, and identifying ways of testing for, the massive states of gravitational waves in extended theories of gravity

A relevant aspect of higher order gravity theories is that, in the post-Minkowskian limit (i.e., with weak fields and arbitrary velocities), the propagation of the gravitational fields turns out to be characterized by waves with both tensorial and scalar modes [41, 42]. This feature represents a striking difference between GR and extended gravity since, in the standard Einstein scheme, only tensorial degrees of freedom are allowed. Gravitational waves represent a fundamental tool to discriminate between GR and alternative gravities [43, 44]. A graviton with non-zero mass produces several effects, such as extra degrees of polarization of gravitational wave modes and a frequency-dependent speed of propagation resulting in a non-trivial dispersion relation. Then, the graviton mass could be constrained using future observations of gravitational waves with the LIGO, Virgo, and the space-based LISA experiments [45, 48]. For example, dynamical binary systems emitting gravitational waves could constitute a good testbed to probe massive gravitons [49, 50]. During their dynamical evolution, the frequency of the binary orbit increases, ramping up rapidly in the late stages of the evolution just before coalescence. Then one proposes a systematic study of gravitational waves for a more general fourth order theory (with the addition of all curvature invariants). Such theories should be analyzed for given sources (for example binary systems) by building models of gravitational emission also for further massive modes of propagation. Today the propagation is studied as a perturbation of Minkowski space (weak gravitational waves), while we can investigate also what the propagation on a curved background (“hard” gravitational waves).

Energy and conservation laws in non-linear (extended) theories of gravity

As seen above, specific tools have been developed to investigate and solve related problems in different areas: weak-field and Newtonian limit, symmetries, Noether’s method, etc. usually based on higher order (non-linear) mathematical models. This proposal intends to open up a new pathway aimed to studying fourth or higher order gravity in the general context of gravitational theories (higher-order in a purely metric and/or non-linear framework, or first-order, with both metric and connection variables - `a la Palatini) in order to allow a more general and unifying treatment of many of the aforementioned topics. Specific attention will be devoted to investigations of the Hamiltonian structure of non-linear (higher order) theories of gravity, with the goal of discussing a more general theory and providing specific examples of conservation laws for exact solutions of these theories. Solutions with singularities (with or without horizons, both standard or generalized) and especially black hole solutions will be approached in order to better understand their entropic properties in presence of standard and dark mass-energy. Another main topic, in the framework of exact approach, is Noether Symmetries [37] and Janis Newman method. By composing two methods it is possible to find axially symmetric solutions starting spherically symmetric ones [39]. Since a real tests of ETGs are also the binary systems (to test the theories at higher energy) and when we consider the physics of rotating systems we must consider a specetime with symmetric properties like Kerr metric, the study of axially symmetric solution is a crucial point.

... while the current status ...

In the last few decades, several issues have arisen in cosmology and Quantum Field Theory which suggest extending Einstein’s theory of General Relativity (GR) in order to cure several shortcomings that manifest themselves in astrophysical observations and fundamental physics. For example, problems in early time cosmology led to the conclusion that the Standard Cosmological Model could be inadequate to describe the universe at extreme regimes [1]. In addition, the Hubble diagram of type Ia supernovae [2, 3], the anisotropy and polarization spectra of the Cosmic Microwave Background Radiation (CMBR) [4], and the matter power spectrum inferred from large structure surveys [5] strongly favour what is now termed the ``Concordance Model’’, namely, a spatially flat universe undergoing an accelerated expansion driven by a dominant component with negative pressure usually referred as dark energy.
Other issues come from astrophysics. For example, the observed Pioneer anomaly problem [6, 7] can be relocated into the same context [8] and then, in addition to cosmology and quantum field theory, a systematic analysis of such theories at small, medium and large scales becomes urgent. In particular, a delicate point consist of the weak-field limit of any extended theory of gravity since two main issues are extremely relevant: i) preserving the successes of GR at local scales since they fit well Solar System experiments and observations; ii) incorporating in a self-consistent and comprehensive picture phenomena such as the anomalous acceleration and dark matter at galactic scales.
Now the paths to solve this conundrum are essentially two: either we go on looking for the dark components till we do actually find them, or else we admit that the cosmic acceleration and the “missing mass’’ problem are nothing but signs that GR is incorrect. Then, a conservative approach could consist of searching for explanations for dark matter and dark energy without introducing exotic forms of mass-energy. A radical alternative, as said, could be that GR is unable to describe the universe at scales larger than the Solar System, and that the dark components could be the observable effect of this inadequacy. Given the above and the lack of a final self-consistent theory of quantum gravity, alternative theories of gravity have been pursued to attempt a semiclassical scheme in which GR and its successes can be recovered. The approach of Extended Theories of Gravity (ETGs), based on corrections and enlargements of the Einstein scheme, have become a sort of paradigm in the study of the gravitational interaction [9 - 15].
From the astrophysical point of view, ETGs do not require finding candidates for dark energy and dark matter at the fundamental level; the approach begins by taking into account only the observed ingredients (i.e., gravity, radiation, and baryonic matter), in agreement with the idea that gravity may not act the same way as in GR at all scales. For example, it is possible to show that several scalar-tensor and so-called f(R) models (where f is a generic function of the Ricci scalar) agree with cosmological and extragalactic observations, and give rise to new effects capable of explaining the observed acceleration of the cosmic fluid and the missing matter effect of self-gravitating structures without the need of introducing dark energy and dark matter [16 - 18].
In this more general scheme, the gravitational action can be modified by replacing the Ricci scalar R with a generic analytic function of all the curvature invariants (Ricci, Riemann and Weyl tensors, and also the d’Alembertian of R and its powers), possibly with extra scalar fields, in general non-minimally coupled with gravity. From the fundamental point of view, such modifications emerge in all the attempts to formulate quantum field theory in curved spacetime, and also as the result of the low-energy limit of string or M-theory.
Even if positive results already exist at the cosmological and extragalactic levels, they are to be considered only as first evidences of Extended Theories of Gravity, which should be accurately tested at all scales. Furthermore the discussion about the short scale behavior of higher order gravity has been quite lively in the last few years since the GR shows its best predictions just at the Solar System level. Measurements coming from weak-field limit tests like the bending of light, the perihelion shift of planets and the frame dragging experiments represent inescapable tests for any theory of gravity. Actually there are sufficient theoretical predictions to state that higher order theories of gravity can be compatible with Newtonian and post-Newtonian prescriptions [19] since the standard Solar System tests can be evaded by several classes of them [20]. Nevertheless, up to now, the discussion on the weak field limit of f(R) theories is far to be definitive and there are several papers claiming for opposite results [21-28], or stating that no progress has been reached in the last forty years due to several misconceptions in the various theories of gravity [29, 30].
However for examples, with reference to a generic f(R) theory, the weak-field, slow motion (Newtonian) limit introduces in the Newtonian potential a Yukawa-like correction term depending on the derivatives of the function f(R) with respect to the Ricci scalar [31-33]. In the post-Minkowskian limit of f(R) gravity, we do not have an energy-momentum pseudo-tensor as in GR, but rather a tensor related to the gravitational field. In Extended Theories of Gravity, is not possible to eliminate the contributions of second order in the Ricci scalar when we perform variations [34]. Note that we have for both limits a correspondence with GR at all levels of the theory (action, field equations, and their solutions) so GR can be easily recovered. These results have been generalized to actions expressed by functions of the Ricci scalar and of the quadratic contractions of the Ricci and Riemann tensors with themselves [35], obtaining a more general but always compatible solution with respect to the previous one.
This approach includes the so-called quadratic gravity models generated by the Lagrangian R + a R^2 + b R_{\alpha\beta}R^{\alpha\beta} justified by quantum field considerations [36]. The corresponding gravitational potential is given by the Newtonian one corrected by two additive exponential terms with ranges related to the parameters (a, b) of the theory (or to derivatives of f with respect to the curvature invariants). For the expected values of the scaling lengths, the modified potential reduces to the Newtonian one on the Solar System scale, in agreement with the classical tests of gravity. The Newtonian limit of f(R) gravity has been investigated also in the Jordan and the Einstein conformal frames using the equivalence between scalar-tensor and f(R) theories [37]. The main result is the failure of the Gauss and Birkhoff theorems to hold [31–34]. The first, and crucial, consequence of the non-validity of these theorems is in the calculation of the gravitational potential, when different sources of the gravitational field exhibit different spatial scales.
Extended Theories of Gravity (in particular f(R) gravity) have been investigated also with the Noether symmetry approach in order to find analytical spherically symmetric solutions [38]; the Newman-Janis method has generated exact axially symmetric solutions (analogous to the Kerr metric) beginning with spherical ones [39].

[1] Buchbinder I.L., Odintsov S.D., Shapiro I.L., Effective action in Quantum Gravity IOP Publishing Bristol (1992)
[2] Perlmutter S., et al., Astrophys. J., 517, 565 (1999)
[3] Riess A.G., et al., Astrophys. J. 607, 665 (2004)
[4] Spergel D.N. et al., Astrophys. J. (Suppl.) 148, 175 (2003)
[5] Bahcall N.A., et al., Science 284, 1481 (1999)
[6] Anderson J.D. et al. Phys. Rev. Lett. 81, 2858 (1998)
[7] Anderson J.D. et al. Phys. Rev. D 65, 082004 (2002
[8] Bertolami O., Bohmer C.G., Harko T., Lobo F.S.N., Phys. Rev. D 75, 104016 (2007)
[9] Weyl H., Math. Zeit. 2, 384 (1918)
[10] Pauli W., Phys. Zeit. 20, 457 (1919)
[11] Bach R., Math. Zeit. 9, 110 (1921)
[12] Weyl H., Raum-Zeit-Materie (Springer, Berlin, 1921)
[13] Eddington A.S.,The Mathematical Theory of Relativity (Cambridge University Press, Cambridge, 1924)
[14] Lanczos C., Z. Phys. 73, 147 (1931)
[15] Buchdahl H.A., Nuovo Cimento 23, 141 (1962)
[16] Capozziello S., Cardone V.F., Troisi A., JCAP 0608, 001 (2006)
[17] Capozziello S., Cardone V.F., Troisi A., Mon. Not. Roy. Astron. Soc. 375, 1423 (2007)
[18] Capozziello S., De Filippis E., Salzano V., arXiv:0809.1882 [astro-ph] (2008)
[19] Capozziello S., Troisi A., Phys. Rev. D 72, 044022, (2005)
[20] Hu W., Sawicki I., Phys. Rev. D 76 064004 (2007)
[21] Sotiriou T. P., Gen. Rel. Grav. 38, 1407 (2006)
[22] Allemandi G., Francaviglia M., Ruggiero M. L., Tartaglia A., Gen. Rel. Grav. 37, 1891 (2005)
[23] Nojiri S., Odintsov S.D., Phys. Lett. B 657, 238 (2007)
[24] Chiba T., Phys. Lett. B 575, 1 (2005)
[25] Clifton T., Barrow J.D., Phys. Rev. D 72, 103005 (2005)
[26] Faraoni V., Phys.Rev. D 74 023529 (2006)
[27] Erickcek A.L., Smith T.L., Kamionkownski M, Phys.Rev. D 74 121501 (2006)
[28] Chiba T., Erickcek A.L., Smith T.L., Phys. Rev. D 75 124014 (2007)
[29] Sotiriou T.P., Faraoni V., Liberati S., Int. J. Mod. Phys. D 17 399 (2008)
[30] Multamaki T., Vilja I., Phys. Rev. D 74, 064022 (2006)
[31] Stabile A., Phys. Rev. D, in press (arXiv:1004.1973)
[32] Capozziello S., Stabile A., Troisi A., Mod. Phys. Lett. A 24, 659 (2009)
[33] Capozziello S., Stabile A., Troisi A., Phys. Rev. D 76, 104019 (2007)
[34] Capozziello S., Stabile A., Troisi A., Int. J. Theor. Phys. 49, 1251 (2010)
[35] Stabile A., submitted to Phys. Rev. D (arXiv:1007.1917)
[36] Capozziello S., Stabile A., Class. Quantum Grav. 26, 085019 (2009)
[37] Capozziello S., Stabile A., Troisi A., Phys. Lett. B 686, 79 (2010)
[38] Capozziello S., Stabile A., Troisi A., Class. Quantum Grav. 24, 2153 (2007)
[39] Capozziello S., De Laurentis M., Stabile A., Class. Quantum Grav. 27, 165008 (2010)
[40] Muno M.P. et al, Astrophys. J. 636, L41 (2006)
[41] Stelle K.S., Gen. Rev. Grav. 9, 343, (1978)
[42] Nishizawa A., Taruya A., Hayama K., Kawamura S., Sakagami M., Phys. Rev. D 79, 082002 (2009)
[43] Maggiore M., Phys. Rep. 331, 283 (2000)
[44] Will C.M., Living Rev. Relativity 9, 3 (2006) (http://www.livingreviews.org/lrr-2006-3 or gr-qc/0510072)
[45] Di Fiore L. et al. (VIRGO collaboration), Nuclear Inst. Meth. A, 289, 518 (1990)
[46] De Rosa R., Di Fiore L, Milano L. and LIGO_VIRGO collaboration, Nature 460, 990 (2009)
[47] Capozziello S., Corda C., De Laurentis M., Phys. Lett. B 669, 255 (2008)
[48] Capozziello S. De Laurentis M., Nojiri S, Odintsov. S.D., Gen. Rel. Grav. 41, 2313 (2009)
[49] Will C.M., Phys. Rev. D 57, 2061-2068 (1998)
[50] Berti E., Buonanno A., Will C.M., Phys. Rev. D 71, 084025 (2005)